RaydiumWikiNi:CommandeBras

II/ Commande des différents moteurs

PLAN

II.1/ Comment fonctionnent-ils? Comment les commander?

II.2/ Fonctions pour simplifier l'utilisation

II.1/ Comment fonctionnent ces servomoteurs?

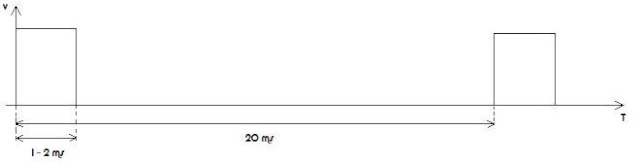
Afin de diriger ces moteurs, il nous faut leur appliquer à chacun une impulsion entre une et deux millisecondes toutes les vingt millisecondes.

Une impulsion d'une milliseconde positionne le servomoteur en butée gauche.
Une impulsion de deux millisecondes positionne le servomoteur en butée droite.
Une impulsion d'une milliseconde et demie positionne le servomoteur au milieu.

Comment commander ces servomoteurs?

Nous utilisons un micro-processeur M32C83.
Nous avons donc deux possibilités pour générer ces impulsions.

Soit en utilisant la fonction PWM (Pulse Width Modulation).
Soit en utilisant un timer que l'on modifie à chaque utilisations.

L'avantage de la PWM est qu'il ne dépend pas du processeur, et donc il y a moins de risque d'erreur.
Mais nécessite six PWM pour commander les sept moteurs.

L'avantage de l'utilisation d'un timer est que l'on peut rajouter des fonctionnalités, car seulement un timer est utilisé ( contrairement à six dans le cas de la PWM).
Mais il sera moins précis, car utilisant des interruptions, certains problèmes peuvent arriver.

II.2/ Fonctions pour simplifier l'utilisation

Nous avons choisit d'utiliser la deuxième méthode, c'est à dire l'utilisation d'un seul timer.

Pour cela nous devons définir deux conditions:

Le temps à appliquer sur chaque moteur
- état haut
- état bas
Le diriger sur le bon port

Les ports que nous avons utilisés pour relier le microcontrôleur et le bras robot sont:

P2_0 Pour le moteur A

P2_1 Pour le moteur B

P2_3 Pour le moteur C

P2_2 Pour le moteur D

P2_4 Pour le moteur E

P2_5 Pour le moteur F

Voici le code que nous avons rédigé pour pouvoir faire ces conditions:

//Variables prédéfinies//
#define MILLISEC 6000
#define REPOS 13200
#define COEFF 44

void timer()
{
	// Variables statiques : la valeur est conservée d'appel en appel //
 
	static int etat=0; // Correspond à l'état du signal à envoyer au moteur //
	static int num=0; // Numéro du moteur cible //
 
	// On sélectionne le port //
	switch (num)
	{
		case 0 : p2_0 = 1 - etat; break;
		case 1 : p2_1 = 1 - etat; break;
		case 2 : p2_3 = 1 - etat; break;
		case 3 : p2_2 = 1 - etat; break;
		case 4 : p2_4 = 1 - etat; break;
		case 5 : p2_5 = 1 - etat; break;
	}

// L'état bas du signal de chaque moteur à une durée constante //
	// Calcul de l'état bas //
	if ( etat == 0 )
	{
		ta1 = REPOS - ta1;
	}
	// L'état haut du signal de chaque moteur dépend de la valeur de l'angle à appliquer //
	// Calcul de l'état haut //
	else
	{
		switch (num)
		{
			case 0 :  ta1= MILLISEC + COEFF*angA;       // Calcul de la valeur de Ta1 pour le moteur A //
				break; 
			case 1 : 	ta1= MILLISEC + COEFF*angB; // Calcul de la valeur de Ta1 pour le moteur B //
				break;
			case 2 : 	ta1= MILLISEC + COEFF*angC; // Calcul de la valeur de Ta1 pour le moteur C //
				break;
			case 3 : 	ta1= MILLISEC + COEFF*angD; // Calcul de la valeur de Ta1 pour le moteur D //
				break;
			case 4 : 	ta1= MILLISEC + COEFF*angE; // Calcul de la valeur de Ta1 pour le moteur E //
				break;
			case 5 : 	ta1= MILLISEC + COEFF*angF; // Calcul de la valeur de Ta1 pour le moteur F //
				break;
		}
		
		if (num++ == 5)	num=0;
	}
	
	// On commute l'état pour passer de l'état haut à l'état bas //
	etat = 1 - etat;
}

Maintenant que nous savons comment contrôler les servomoteurs, nous allons voir comment calculer les valeurs des angles à leurs envoyer.
Pour ceci, nous avons le choix entre deux méthodes:
- Les matrices de déplacement
- La méthode géométrique

II.3/ Matrice de déplacement

ICI

II.4/ La méthode géométrique

Afin de positionner la pince grâce aux coordonnées (X1, Y1, Z1), nous sommes passés par un calcul géométrique.

Nous avons décidé de laisser la pince à l'horizontale, ce qui nous permet de calculer que trois angles.

A , ( le moteur A du bras )
B , ( le moteur B du bras )
C , ( le moteur C du bras )

Afin de calculer A nous allons utiliser la tangente:

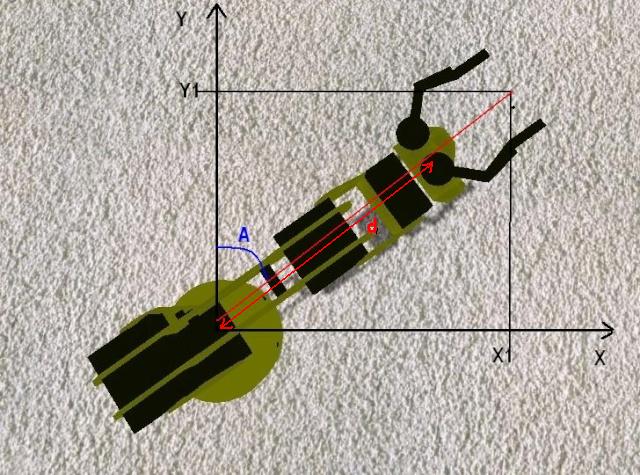
A = Arc tangente ( X1 / Y1 )

d² = X1² + Y1²

Calcul de d, et de l'angle à appliquer pour le moteur A

if (coorX == 0)
			{
				if (coorY < 18) coorY = 18;
				d = coorY - 13; // On enlève les 13 cm de la pince //
				angA_cons = 0;
			}
		else if (coorY == 0)
			{
				if (coorX > 0)
					{
						if (coorX < 18) coorX = 18;					
						angA_cons = 90;
					}
				else if (coorX < 0)
					{
						if (coorX > -18) coorX = -18;
						angA_cons = -90;
					}
				
				d = abs(coorX) - 13;	
			}
		else if (sqrt( (coorX*coorX) + (coorY*coorY)) > 18)
			{
				d = sqrt( (coorX*coorX) + (coorY*coorY))-13; 
				angA_cons = atan(coorX/coorY)*(180/PI);
			}

Maintenant que nous avons calculé d et A, nous pouvons passer à la suite:

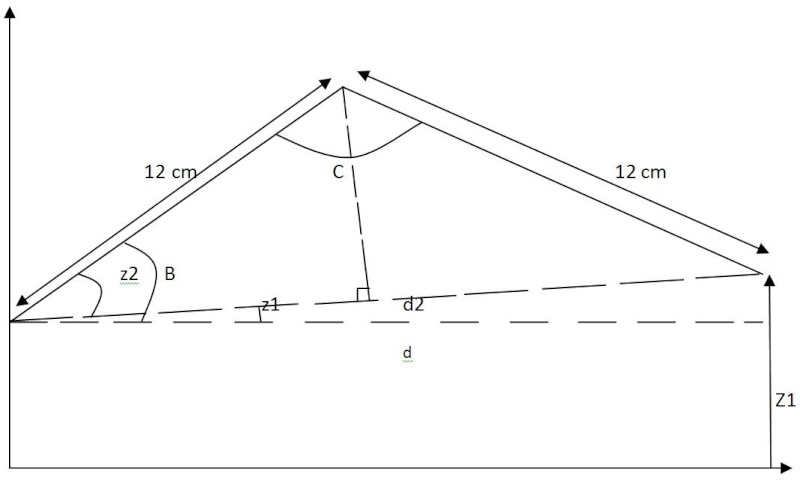
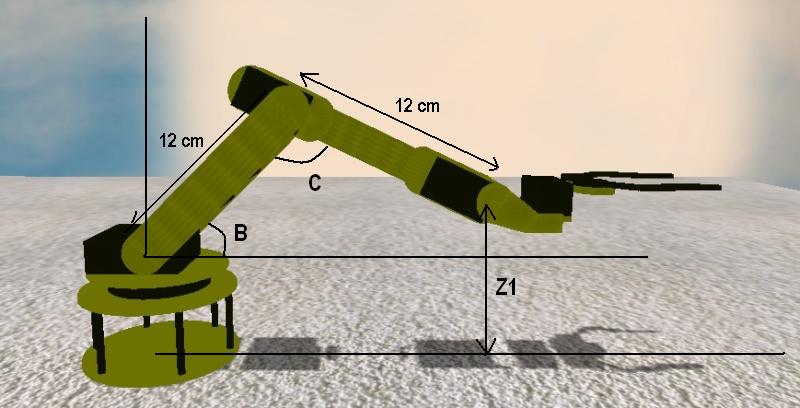
d2² = d² + ( Z1 - 8 ) Z1 - 8 sert à enlever la base pour calculer à partir du point de pivot B

z1 = Arc tangente ( ( Z1 - 8) / d )
z2 = Arc sinus ( racine ( 12² - ( d2 / 2 )² ) / 12 )

B = z1 + z2

C = 2 * Arc sinus ( ( d2 / 2 ) / 12 )
C = 2 * Arc sinus ( d2 / 24 )

Calcul de d2

d2 = sqrt( (d*d) + ((coorZ-8)*(coorZ-8)));

Calcul de l'angle à appliquer pour le moteur B

if (d2 <= 24) // 24 == longueur maximum de d2 (12 + 12) 
			{
				
				z1 = atan((coorZ-8)/d)*(180/PI);
				z2 = asin(sqrt(144 - (d2/2)*(d2/2))/12.0f)*(float) (180.0f/PI);
 
				angB_cons = (z1 + z2);

Calcul de l'angle à appliquer pour le moteur C

angC_cons = -(2*(asin(d2/24.0f)*(float) (180.0f/PI))-90);

Arrivé à ce point, nous pouvons positionner le point de pivot ou l'on veut.
Il nous reste plus qu'à calculer D, l'angle à appliquer au moteur D afin que la pince soit toujours horizontale.

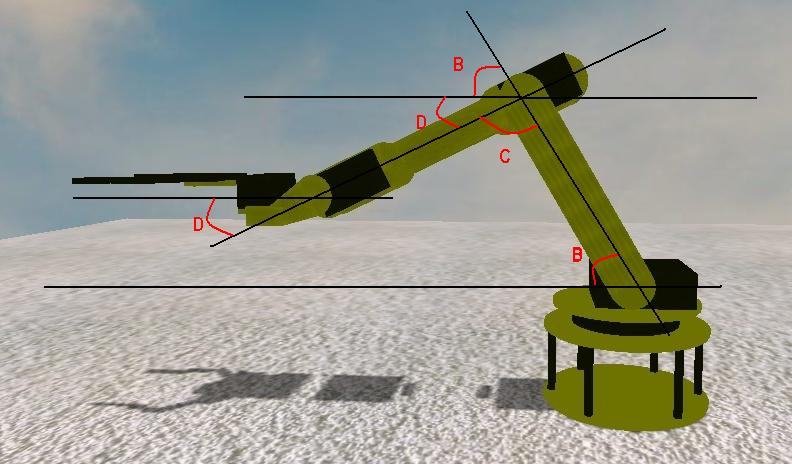
on a :

D + B + C = 180
D = 180 - B - C

Mais vu que sur le robot l'angle moteur C = 0 correspond à un angle de 90°
D = 180 - B + ( 90 - C)

Calcul de l'angle à appliquer pour le moteur D

angD_cons = -(angB_cons +(90-angC_cons)) + 170;
 // 180 - 10 car la pince n'est pas à 0 Pour l'angle 0 //

Retour