II.3/ Matrice de déplacement
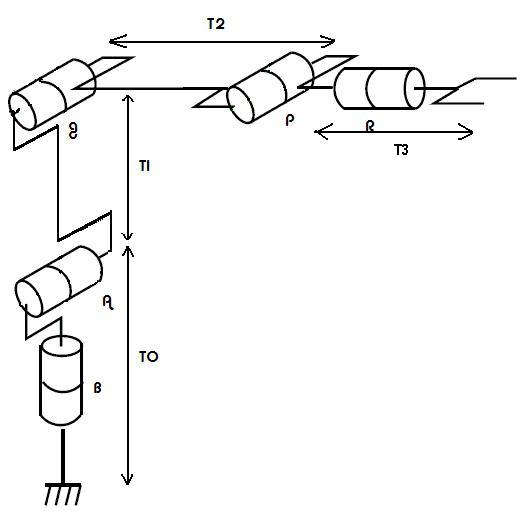
Nous disposons de deux types de matrices:
- les matrices de rotation
- les matrices de translation
Les matrices:
En commençant par l'origine du robot.
Une matrice de translation sur z de 8 cm T0:
|1 0 0 0|
|0 1 0 0|
|0 0 1 8|
|0 0 0 1|
|0 1 0 0|
|0 0 1 8|
|0 0 0 1|
Une matrice de rotation Rz A:
|cosB -sinB 0 0|
| sinB cosB 0 0|
| 0 0 1 0|
| 0 0 0 1|
| sinB cosB 0 0|
| 0 0 1 0|
| 0 0 0 1|
Une matrice de rotation Rx B:
|0 0 0 0|
|0 cosA -sinA 0|
|0 sinA cosA 0|
|0 0 0 1|
|0 cosA -sinA 0|
|0 sinA cosA 0|
|0 0 0 1|
Une matrice de translation sur y de 12 cm T1:
|1 0 0 0 |
|0 1 0 12 |
|0 0 1 0 |
|0 0 0 1 |
|0 1 0 12 |
|0 0 1 0 |
|0 0 0 1 |
Une matrice de rotation Rx C:
|0 0 0 0|
|0 cosG -sinG 0|
|0 sinG cosG 0|
|0 0 0 1|
|0 cosG -sinG 0|
|0 sinG cosG 0|
|0 0 0 1|
Une matrice de translation sur z de -12 cm T2:
|1 0 0 0 |
|0 1 0 0 |
|0 0 1 -12|
|0 0 0 1 |
|0 1 0 0 |
|0 0 1 -12|
|0 0 0 1 |
Une matrice de rotation Rx E:
|0 0 0 0|
|0 cosP -sinP 0|
|0 sinP cosP 0|
|0 0 0 1|
|0 cosP -sinP 0|
|0 sinP cosP 0|
|0 0 0 1|
Une matrice de translation sur z de -13 cm et sur y de 8 cm T3:
|1 0 0 0 |
|0 1 0 8 |
|0 0 1 -13|
|0 0 0 1 |
|0 1 0 8 |
|0 0 1 -13|
|0 0 0 1 |
Il nous reste deux matrices à faire, celles ci serviront juste à régler l'inclinaison de la pince, et l'ouverture ou fermeture de celle ci.
A partir de ce point nous avons le moyen de positionner la pince avec des angles voulus.
Voici la matrice obtenue une fois les multiplications effectuées :
T0 x A x B xT1 x C x T2 x E x T3 =
| cos(b) | (-sin(b)* cos(a)* cos(g)+ sin(b)* sin(a)* sin(g))* cos(p)+ (sin(b)* cos(a)* sin(g)+ sin(b)* sin(a)* cos(g))* sin(p) | -(-sin(b)* cos(a)* cos(g)+ sin(b)* sin(a)* sin(g))* sin(p)+ (sin(b)* cos(a)* sin(g)+ sin(b)* sin(a)* cos(g))* cos(p) | 9*(-sin(b)* cos(a)* cos(g)+ sin(b)* sin(a)* sin(g))* cos(p)+ 9*(sin(b)* cos(a)* sin(g)+ sin(b)* sin(a)* cos(g))* sin(p)+12*(-sin(b)* cos(a)* cos(g)+ sin(b)* sin(a)* sin(g))* sin(p) -12*(sin(b)* cos(a)* sin(g)+ sin(b)* sin(a)* cos(g))* cos(p) -12* sin(b)* cos(a)* sin(g) -12*sin(b)* sin(a)* cos(g) -12*sin(b)* cos(a) |
| sin(b) | (cos(b)* cos(a)* cos(g)- cos(b)* sin(a)* sin(g))* cos(p)+ (-cos(b)* cos(a)* sin(g)- cos(b)* sin(a)* cos(g))* sin(p) | -(cos(b)* cos(a)* cos(g)- cos(b)* sin(a)* sin(g))* sin(p)+ (-cos(b)* cos(a)* sin(g)- cos(b)* sin(a)* cos(g))* cos(p) | 9*(cos(b)* cos(a)* cos(g)- cos(b)* sin(a)* sin(g))* cos(p)+ 9*(-cos(b)* cos(a)* sin(g)- cos(b)* sin(a)* cos(g))* sin(p)+ 12*(cos(b)* cos(a)* cos(g)- cos(b)* sin(a)* sin(g))* sin(p) -12*(-cos(b)* cos(a)* sin(g)- cos(b)* sin(a)* cos(g))* cos(p)+ 12*cos(b)* cos(a)* sin(g)+ 12*cos(b)* sin(a)* cos(g)+ 12*cos(b)* cos(a) |
| 0 | (sin(a)* cos(g)+ cos(a)* sin(g))* cos(p)+ (-sin(a)* sin(g)+ cos(a)* cos(g))* sin(p) | -(sin(a)* cos(g)+ cos(a)* sin(g))* sin(p)+ (-sin(a)* sin(g)+ cos(a)* cos(g))* cos(p) | 7+9*(sin(a)* cos(g)+ cos(a)* sin(g))* cos(p)+ 9*(-sin(a)* sin(g)+ cos(a)* cos(g))* sin(p)+ 12*(sin(a)* cos(g)+ cos(a)* sin(g))* sin(p) -12*(-sin(a)* sin(g)+ cos(a)* cos(g))* cos(p)+ 12*sin(a)* sin(g) -12*cos(a)* cos(g)+ 12*sin(a) |
| 0 | 0 | 0 | 1 |
Prenons un exemple :
b = 0
a = 90
g = 0
p = 0
La matrice devient :
| 1 | 0 | 0 | 0 |
| 0 | cos(90) | -sin(90) | 20*cos(90)+25*sin(90) |
| 0 | sin(90) | cos(90) | 8+20*sin(90)-25*cos(90) |
| 0 | 0 | 0 | 1 |
Ce qui correspond bien à une rotation de 90° suivant l'axe X dont et d'une translation de 25 sur y, et de 28 sur z.
Un problème subsiste, le but de ce projet et de lui donner des coordonnées x y z, et le robot doit calculer l'angle à appliquer au moteur.Il y a trop de variables aléatoires pour résoudre ce problème dans le temps imparti.
Donc nous avons procédé par une http://wiki.raydium.org/wiki/CommandeBras#position
Retour